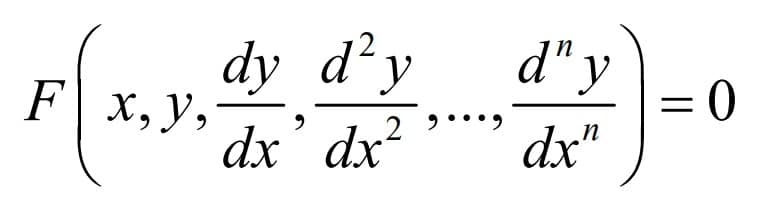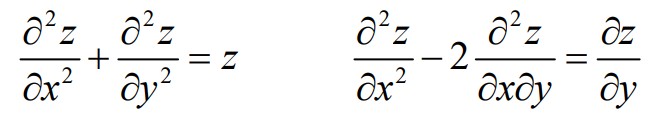Diferansiyel denklemler dersi temel mühendislik dersi olarak mühendislik fakültelerinde gösterilen, ancak öğrenciler tarafından çoğunlukla tek derse kadar gidebilen bir derstir. Aslında tecrübe kazandıkça kolaylaşır ama bir çoğumuz ” Ne işimize yarayacak bu hayatta” sorusu yüzünden öğrenemiyoruz.
Bu başlığı aslında sadece dif. denk. için değil, diferansiyel denklemler gibi bir çok ders üniversite hayatımızda hepimizin korkulu rüyası olmuş tüm derslerimiz için yazdım. Dersler bazen dert olmuş, okulun bitmesine engel olmuştur. Aslında engel bizim kafamızda oluşturduğumuz bu zor gerçekten anlamıyorumdur. Bu yazıyı henüz okulu bitiremeyen bir meslektaş adayımızla geçen gün yaptığımız sohbet üzerine yazma gereği duydum.
Daha önce de defalarca hangi dersin kötü sorusuna aldığım cevapların %80 %90’ı diferansiyel denklemler veya türevleri oldu. (Türev demişken integrali de yabana atmayalım) Kelime olarak kullanmak oldukça kolay olsa da, bu dersler evet zor ama binlerce mühendis diploma almaya hak kazandığına göre başarılamaz değiller. Onlarca hocamız ise hala bunlarla çalışıyor ve makale tez yazıyor. Bir dersi dert haline getirmek çoğunlukla bizim umarsızlığımızdan ve ilgisizliğimizden kaynaklanıyor. Öğrenci arkadaşlar, mühendis olacaksanız bu dersi geçeceksiniz. Sohbet ettiğim arkadaşım gibi 6. senenizde diferansiyel denklemleri veremiyorsanız, senelerce okul için harcadığınız maddi miktara ve manevi olarak kaybettiğiniz zamana bir bakın. Şuraya diferansiyel denklemlerin tanımlamasını bırakayım da artık bir noktadan başlayın ve bitirin.
Diferansiyel denklemler;
Bir y = f(x) fonksiyonunun, x serbest değişkeni, y bağlı değişkeni ve onun sınırlı sayıda herhangi mertebeye kadar türevleri arasında kurulmuş olan bir bağıntıya Diferansiyel Denklem denir. Bu tanıma göre bir diferansiyel denklemin genel ifadesi şu şekildedir:
Buradaki tanım, genel anlamda tüm diferansiyel denklemleri kapsamış olsa da uygulamada çok farklı durumlarla karşılaşılır. Özellikle çözüme yönelik formları oluştururken, daha farklı ve özel düzenlerin tanımlandığına tanık olacağız. Buna bağlı olarak çözüm kavramı da ayrıca konu edilmeyi gerektirecektir. Yukarıdaki tanımda sözü edilen denklemlere, tek bir serbest değişken ile kuruldukları için Adi Diferansiyel Denklem ya da sadece Diferansiyel Denklem denir. Diferansiyel denklem denilince, kendiliğinden, Adi Diferansiyel Denklemler anlaşılacaktır.
z = f(x,y) gibi iki serbest değişkeni olan bir fonksiyon söz konusu ise bunun türevleri ∂z/∂x; ∂z/∂y şeklinde ifade edileceğinden, bunlarla elde edilecek diferansiyel denklemler de bu tür türevleri içerecektir. Bunlara Kısmi Türev denildiği için, bunlarla oluşacak diferansiyel denklemlere de Kısmi Türevli Diferansiyel Denklemler ya da sadece Kısmi Diferansiyel Denklemler denir. Aşağıda bu tür denklemler için iki örnek gösterilmiştir.
Mühendis adam sıfırdan başlasa bile her şeyi öğrenip uygulayabilecek olandır. Çokta uzatmayın, uzatmayalım… Saygılarımla.